How To Factor Perfect Cube
Factoring the Sum and Difference of Two Cubes
In algebra class, the teacher would always discuss the topic ofsum of two cubes and divergence of two cubes next. The reason is that they are similar in construction. The cardinal is to "memorize" or remember the patterns involved in the formulas.
- Case ane: The polynomial in the grade {a^iii} + {b^3} is called the sum of ii cubes considering two cubic terms are existence added together.
- Case ii: The polynomial in the form {a^3} - {b^3} is called the difference of ii cubes considering 2 cubic terms are being subtracted.
Then here are the formulas that summarize how to factor the sum and difference of two cubes. Written report them carefully.
Case 1: Sum of Two Cubes

Observations:
- For the "sum" case, the binomial factor on the right side of the equation has a middle sign that is positive.
- In addition to the "sum" case, the eye sign of the trinomial factor volition always be contrary the middle sign of the given problem. Therefore, it is negative.
Case 2: Deviation of Two Cubes

Observations:
- For the "deviation" instance, the binomial factor on the right side of the equation has a middle sign that is negative.
- In addition to the "divergence" case, the heart sign of the trinomial gene will ever be opposite the middle sign of the given problem. Therefore, it is positive.
Examples of How to Factor Sum and Departure of Ii Cubes
Let's go over some examples and come across how the rules are applied.
Case 1: Factor {10^3} + 27.
Currently, the problem is non written in the form that we want. Each term must exist written as a cube, that is, an expression raised to a power of iii. The term with variable x is okay but the 27 should be taken care of. Obviously, we know that 27 = \left( three \right)\left( three \right)\left( 3 \correct) = {3^3}.
Rewrite the original problem as sum of two cubes, and and then simplify. Since this is the "sum" case, the binomial factor and trinomial factor volition have positive and negative center signs, respectively.
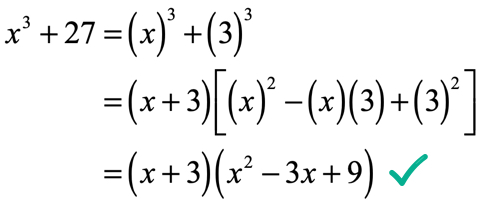
Instance 2: Factor {y^iii} - 8.
This is a instance of difference of two cubes since the number 8 can be written as a cube of a number, where viii = \left( 2 \right)\left( ii \correct)\left( 2 \correct) = {ii^3}.
Apply the rule for divergence of two cubes, and simplify. Since this is the "departure" example, the binomial cistron and trinomial factor volition take negative and positive middle signs, respectively.
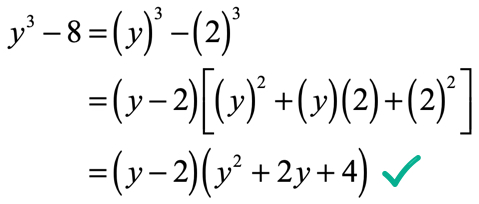
Example three: Factor 27{x^3} + 64{y^iii}.
The first step as always is to express each term as cubes. We know that 27 = {three^3} and 64 = {4^iii}. Rewrite the trouble as
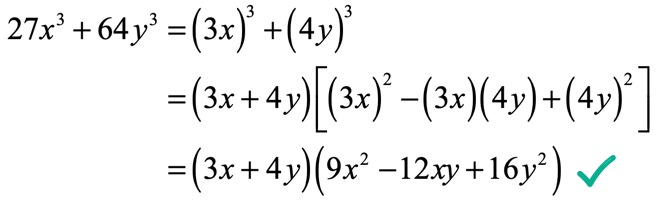
Instance 4: Factor 125{ten^three} - 27.
Since 125 = \left( 5 \right)\left( v \right)\left( 5 \correct) = {5^3} and 27 = \left( 3 \right)\left( three \right)\left( 3 \correct) = {three^three}, this is conspicuously a problem on difference of 2 cubes.
Here's the solution.
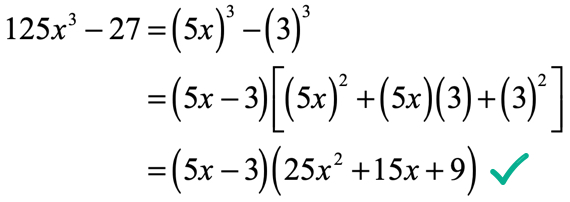
Example 5: Factor 1 - 216{x^iii}{y^three}.
At first, this problem may look "difficult". However, if you stick to what we know already nearly sum and difference of two cubes nosotros should be able to recognize that this problem is rather easy.
The proficient thing is that the variables are cubes then they are fine. At present for the number, it is piece of cake to see that that 1 = \left( 1 \correct)\left( 1 \right)\left( 1 \right) = {i^3} while 216 = \left( 6 \right)\left( half-dozen \correct)\left( half-dozen \right) = {6^iii}. This is actually a case of departure of two cubes.
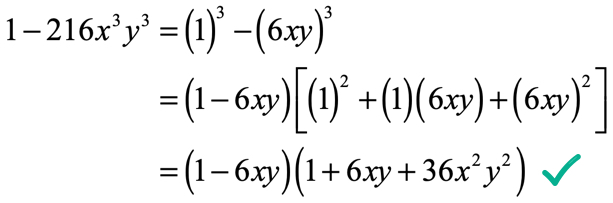
Example vi: Factor 8{x^6}{y^{12}} + 27.
This problem is a bit unlike. The coefficients are definitely cubes because 8 = {2^3} and 27 = {3^three}. Now, how practise we limited the term with variables as a cube? Well, simply gene out 3 from the existing exponents of "x" and "y". Use the law of exponent known as Power to a Power Dominion to justify this step. We take out three because to exist a cube implies that any expression must have an outer exponent of iii.
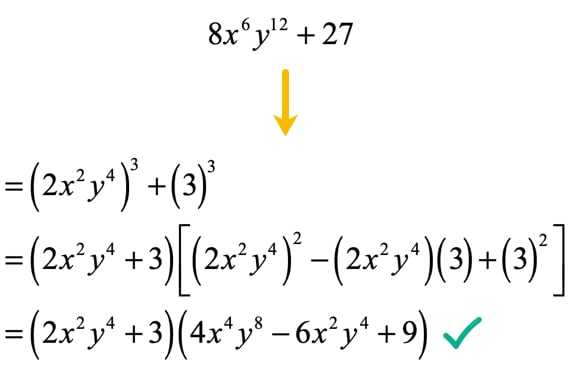
Example 7: Gene 3xy - 24{ten^iv}y.
Sometimes the problem may not appear to be factorable by either sum or difference of two cubes. If you run across something similar this, try to take out mutual factors. For the numbers, the greatest common factor is 3 and for the variables, the greatest common factor is "xy". Therefore the overall mutual cistron would exist their product which is \left( three \right)\left( {xy} \correct) = 3xy.
After factoring it out, y'all'll see that nosotros take an like shooting fish in a barrel problem on the difference of two cubes.
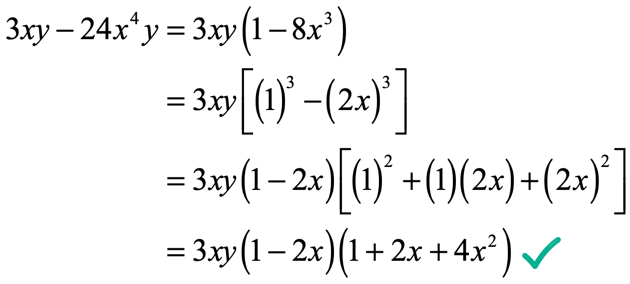
You might too be interested in:
Factoring Difference of Two Squares
Factoring Difference of Ii Squares Practice Problems
Factoring Sum and Difference of Two Cubes Practice Problems
How To Factor Perfect Cube,
Source: https://www.chilimath.com/lessons/intermediate-algebra/factoring-sum-and-difference-of-two-cubes/
Posted by: dentoncorties.blogspot.com


0 Response to "How To Factor Perfect Cube"
Post a Comment