Area Of A Lune Formula

Let'southward turn away from the symbolic mysteries of crescents and investigate them mathematically.

A circle offers a plethora of exciting calculations and geometrical concepts. Starting with easy calculations virtually area and circumference, one soon ends up excavation deeper with topics like semicircles, sectors, segments, and arcs. Permit'south expand our circumvolve knowledge by the calculation of the area of a lune and a crescent.

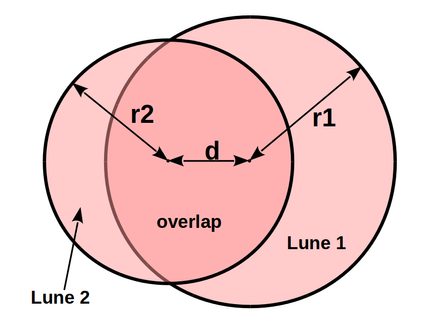
Image of two overlapping circles with radius 1 and 2, distance between circle centers, crescent 1 and 2, and overlapping area marked.

The image above displays ii overlapping circles. Marked are r1 and r2, the radii of the circles 1 and ii respectively, and the distance d between the circumvolve'south centers. The circle'south arcs form the lune areas i and 2 and the overlapping expanse.

The expanse for the lune of circle 1 is can exist computed equally::

lune_1 = two*(√( (r1+r2+d) * (r2+d-r1) * (d+r1-r2) * (r1+r2-d) )/ iv) + r1² * arccos( (r2²-r1²-d²) / (2*r1*d) ) - r2² * arccos( (r2²+d²-r1²) / (2*r2*d) )

If you want to understand this equation meliorate, check out our arccos and square root calculators which provide detailed explanations.

Knowing the area of the lune, we can calculate the overlapping area of the ii circles by subtracting the lune from the total expanse of circumvolve 1:

overlap_area = π*r1² - lune_1

And since the second circle consists of the 2d lune and the mutual overlap area, nosotros calculate the area of the lune of circle two with the same formula:

lune_2 = π*r2² - overlap_area

The source for the formulas above is Eric Weisstein's work on Wolfram MathWorld.